Distributionally Robust Optimization For Language Modeling

Backgrounds

Datasets for training language models (LMs) are typically sampled from a mixture of many domains. For example, the Pile, a large publicly available dataset, is composed of 24% web data, 9% Wikipedia, 4% GitHub, etc. Llama 3.1 is trained with roughly 50% of tokens corresponding to general knowledge, 25% of mathematical and reasoning tokens, 17% code tokens, and 8% multilingual tokens. The mixture proportions of pretraining data domains greatly affect language model (LM) performance. However, it is unclear how much of each domain to include to produce a model that performs well for a wide variety of downstream tasks. To ensure model performance on as many downstream tasks as possible, it is natural to use DRO methods (Distributionally Robust Optimization) to optimize our LMs.

Distributionally Robust Optimization

The standard training procedure for neural networks is called empirical risk minimization (ERM):

\[\hat{\theta}_{\rm{ERM}}=\underset{\theta}{\operatorname{argmin}} \mathbb{E}_{(x, y) \sim \hat{P}} \left[l(f(x;\theta),y)\right],\]

where \(\hat{P}\) is the empirical distribution of the training data \(x\) and \(y\), \(l\) is the loss function, and \(f\) is the neural network parameterized with \(\theta\).

In distributionally robust optimization (DRO), we aim instead to minimize the worst-case expected loss over an uncertainty set of distributions \(\mathcal{Q}\):

\[\min_{\theta}\{\mathcal{R}(\theta):=\sup_{Q\in\mathcal{Q}}\mathbb{E}_{(x, y) \sim Q} \left[l(f(x;\theta),y)\right]\}\]

The uncertainty set \(\mathcal{Q}\) encodes the possible test distributions that we want our model to perform well on. Conventionally, the construction of the uncertainty set \(\mathcal{Q}\) is based on some distance metrics in the following form:

\[\mathcal{Q}:=\{Q\mid Q:d(Q,\hat{P})<=\gamma\},\]

where \(d\) is a distance metric, \(\hat{P}\) is the empirical distribution of the training data \(x\) and \(y\) and \(\gamma\) is a hyperparameter. The distance metric \(d\) can be chosen from a variety of distance metrics, such as the Wasserstein distance and the f-divergence. Generally, if the downstream task apears in the uncertainty set, the model will have satisfactory results. However, based on the distance metric, the construction of the uncertainty set could be over-pessimistic, i.e., it could include some noise distributions which would never appear in the downstream tasks. The over-pessimisim problem would undermine the performance of the model on downstream tasks.

Group DRO

To construct a realistic set of possible test distributions without being overly conservative, we can leverage prior knowledge of spurious correlations to define groups over the training data and then define the uncertainty set \(\mathcal{Q}\) in terms of these groups. Assume the training distribution \(\hat{P}\) is assumed to be a mixture of \(m\) groups \(P_g\) indexed by \(\mathcal{G}=\{1,2,\cdots,m\}\). We can then define the uncertainty set \(\mathcal{Q}\) as any mixture of these groups:

\[\mathcal{Q}:=\{\sum_{g=1}^{m}q_gP_g,q\in\Delta_{m-1}\},\]

where \(\Delta_{m-1}\) is the \(m\)-dimensional simplex. Then the DRO objective can be converted to:

\[\hat{\theta}_{\text{DRO}} := \arg\min_{\theta \in \Theta} \{ \hat{\mathcal{R}}(\theta) := \max_{g \in \mathcal{G}} \mathbb{E}_{(x,y) \sim \hat{P}_g} [\ell(\theta; (x,y))] \}.\]

DRO for Language Modeling

The vanilla methodology still has some limitations, especially in the field of language modeling, where we try to minimize the log loss of a next token prediction.

Consider a multi-task setting, where we have a hard task and a easy task. During training, the hard task already has a rather good performance, and the easy task is still far from optimal. However, in terms of absolute performance, the easy task is still better than the hard task. In such case, previous paradigms would still mainly focusing on optimizing the hard task, though it is already well-optimized. Here comes the key point:

Given that each task has its own difficulty, it would be unfair to optimize these tasks towards the same objective - minimize the loss to 0.

As a result, DRO for LM adds a baseline loss for compensation. Suppose for a given task \(z\), we are fully aware of its performance upper-bound \(p_{x\mid z}(x\mid z)\), we can optimize the task by a baselined loss:

\[l(x,z;\theta)=\log{p_{x\mid z}(x\mid z)}-\log{p_\theta(x)}={\rm{KL}}(p_{x\mid z}(x\mid z)\parallel{p_\theta(x)}).\]

Generally, \(\log{p_{x \mid z}(x \mid z)}\) is hard to estimate, in practice, we can train a baseline model (like bigram model) for each task.

Doremi

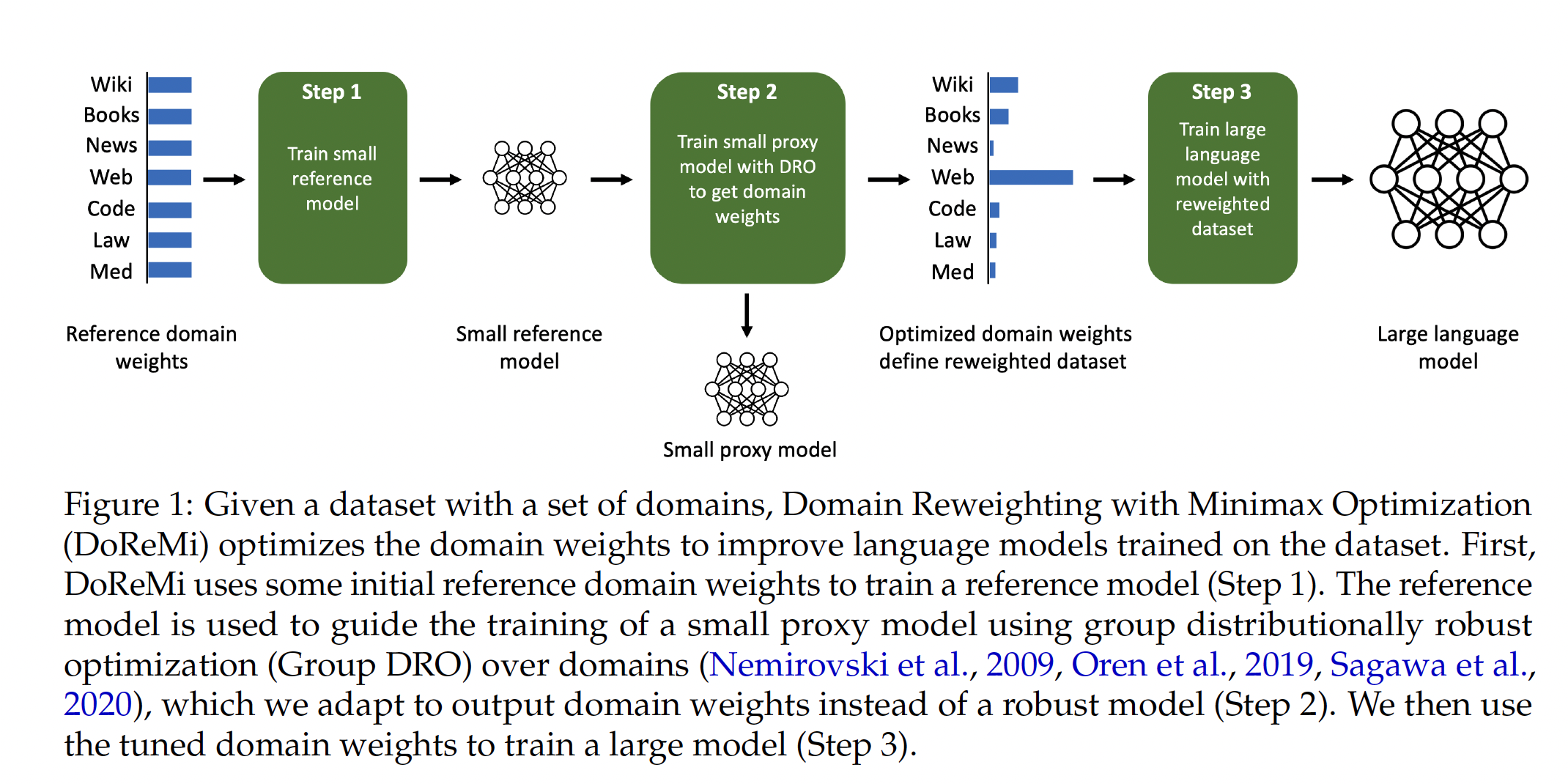
To better use DRO LM training larger language models (like &B or larger), Doremi trains small models with DRO LM to get the domain weights and then uses the weights to train the final model. The overall framework is shown below: